Ik vond ergens op mijn harddisk nog een oud werkstuk uit medio 1995.
De inhoud is klassiek, dus nog steeds aktueel. Google bestond nog niet, in die tijd was Altavista de zoekmachine.
Aangezien alle links en referenties uit het werkstuk ook uit medio 1995 stammen, zullen vele ervan niet meer bestaan of de toenmalige inhoud bevatten ;-)
Toen ik tijdens de bouw van deze site Recursive dit werkstuk weer terugvond, dacht ik dat het wellicht interessant zou zijn om online te zetten. Zeker informatica studenten kunnen hiermee wellicht hun voordeel doen.
Cryptografie betekent primair geheimschrift (Grieks: kryptos [geheim] en grafia [schrift]). Daarnaast staat de wetenschap en de kunst van het geheimschrift ook als cryptografie bekend. Cryptografen houden zich bezig met methoden om gewone tekst om te zetten in geheimschrift en vice versa.
De eerste cryptografen leefden zo'n 4000 jaar geleden in het oude Egypte waar sommige hierogliefen op monumenten gecodeerd werden (zie [ 1 , 2 ]). Ook andere oude beschavingen, ondermeer in Mesopotamie, India en China ontwikkelden geheimschrift. De details met betrekking tot de oorsprong en vroege evolutie van cryptografie - of geheimschrift - zijn echter onbekend.
Het doel van cryptografie was - en is nog steeds - het voorkomen dat derden kennis nemen van berichten die niet voor hen bedoeld zijn. Hiertoe wordt een bericht versleuteld op een manier die - hopelijk - slechts bij de afzender en de rechtmatige ontvanger bekend zijn. Cryptografie werd voornamelijk door heersers, militairen en diplomaten gebruikt.
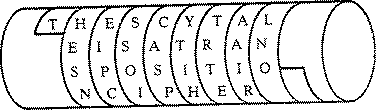
Rond het jaar 400 voor onze jaartelling, kenden de Spartanen een geheimschrift dat gebaseerd was op een scytale.

Een scytale
Dit geheimschrift werd gebruikt door de spartaanse krijgsheren om strategische en tactische informatie uit te wisselen. Een scytale is een cylinder waar een perkamenten lint omheen gewikkeld werd. Op dit perkamenten lint werd de boodschap geschreven. Het lint werd vervolgens van de cylinder verwijderd en aan de bode mee gegeven. Omdat de boodschap op het perkamenten lint slechts leesbaar kon worden gemaakt met behulp van een gelijksoortige scytale, was dit systeem redelijk veilig. De bode kon het bericht niet lezen (zo de bode al kon lezen) en iemand die de boodschap onderschepte waarschijnlijk ook niet. Met een gelijksoortige scytale wordt een scytale met dezelfde diameter bedoeld (zie [ 5 , 8 ]).
Ook de Romeinen kenden geheimschrift. Het verhaal gaat dat Julius Caesar zijn boodschappers niet vertrouwde en daarom in zijn boodschappen iedere 'A' door een 'D' verving, iedere 'B' door een 'E', enzovoorts (zie [ 3 ]). Iedere letter van het alfabet werd vervangen door het - cyclisch - derde daaropvolgende karakter. Bijvoorbeeld:
VENI VIDI VICI
coderen met de Caesar cipher geeft als resultaat:
YHQL YLGL YLFL
Alleen diegenen die de `schuif drie karakters terug`-regel kenden, waren in staat het bericht te lezen. Julius Caesar wordt gezien als een van de eerste personen die cryptografie gebruikte om zijn boodschappen te beveiligen (zie [ 4 ]). De methode die door Julius Caesar gebruikt werd, staat nog steeds bekend als de Caesar cipher.
In de laatste helft van de middeleeuwen nam het gebruik van geheimschrift toe. Ene Roger Bacon heeft ca 1200 diverse versleutelingsmethoden beschreven (zie [ 1 ]). En het werk dat toegeschreven wordt aan Geoffrey Chauser, The Equatorie of the planetris (ca 1390), bevat versleutelde passages.
In 1470, publiceerde Leon Battista Alberti Tattati in cifra waarin hij een cipher disk of cipher wheel beschrijft, waarmee een tekst kon worden versleuteld (zie [ 1, 2, 7 , 8 ]). Een cipher disk is een schijf bestaande uit een aantal concentrische tekstcirkels. Een van deze concentrische cirkels werd gebruikt om de letters uit de tekst mee te selekteren, terwijl een andere gebruikt werd om de bijbehorende gecodeerde letter van af te lezen (zie [ 8 ]).
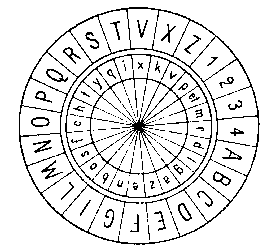
Leon Battista Alberti's cipher disk
Door de letter uit de tekst te vervangen door de letter uit de onderste letter-ring op de disk, kon een tekst worden gecodeerd (zie [ 8 ]). Het coderen van bijvoorbeeld:
BATTISTA
geeft de volgende gecodeerde tekst bij gebruik van bovenstaande cipher disk:
ldiibqid
De authoriteiten op het gebied van cryptografie beschouwen Johannes Trithemius, abt van Spanheim in Duitsland, echter als vader van de moderne cryptografie. In 1510 schreef Trithemius de Polygraphia, het eerste gedrukte werk over cryptologie. Cryptologie is de leer der geheimschriften en bestaat uit drie subdisciplines (zie [ 6 ]):
In 1585 publiceerde Blaise de Vigenère een boek over cryptology, waarin hij een poly-alfabetische substitutie versleuteling beschrijft. Deze versleutelingsmethode staat nog steeds bekend als de Vigenere cipher (zie [ 4 ]). De methode maakt gebruik van het zogenaamde Vigenere tableau. Dit is in essentie een matrix waarbij in de regels op verschillende wijze gerangschikte alfabetten staan. Bij het versleutelen van een tekst worden de verschillende rijen gebruikt om de verschillende substituties te verwezenlijken. Het tableau was als volgt ingedeeld:
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z A A B C D E F G H I J K L M N O P Q R S T U V W X Y Z B B C D E F G H I J K L M N O P Q R S T U V W X Y Z A C C D E F G H I J K L M N O P Q R S T U V W X Y Z A B D D E F G H I J K L M N O P Q R S T U V W X Y Z A B C E E F G H I J K L M N O P Q R S T U V W X Y Z A B C D F F G H I J K L M N O P Q R S T U V W X Y Z A B C D E G G H I J K L M N O P Q R S T U V W X Y Z A B C D E F H H I J K L M N O P Q R S T U V W X Y Z A B C D E F G I I J K L M N O P Q R S T U V W X Y Z A B C D E F G H J J K L M N O P Q R S T U V W X Y Z A B C D E F G H I K K L M N O P Q R S T U V W X Y Z A B C D E F G H I J L L M N O P Q R S T U V W X Y Z A B C D E F G H I J K M M N O P Q R S T U V W X Y Z A B C D E F G H I J K L N N O P Q R S T U V W X Y Z A B C D E F G H I J K L M O O P Q R S T U V W X Y Z A B C D E F G H I J K L M N P P Q R S T U V W X Y Z A B C D E F G H I J K L M N O Q Q R S T U V W X Y Z A B C D E F G H I J K L M N O P R R S T U V W X Y Z A B C D E F G H I J K L M N O P Q S S T U V W X Y Z A B C D E F G H I J K L M N O P Q R T T U V W X Y Z A B C D E F G H I J K L M N O P Q R S U U V W X Y Z A B C D E F G H I J K L M N O P Q R S T V V W X Y Z A B C D E F G H I J K L M N O P Q R S T U W W X Y Z A B C D E F G H I J K L M N O P Q R S T U V X X Y Z A B C D E F G H I J K L M N O P Q R S T U V W Y Y Z A B C D E F G H I J K L M N O P Q R S T U V W X Z Z A B C D E F G H I J K L M N O P Q R S T U V W X Y
Merk op dat iedere regel van de tabel in essentie correspondeert met een Caesar cipher, met dien verstande dat de verschuiving afwijkt van de oorspronkelijke Caesar cipher. De Vigenere cipher gebruikt dit tableau (tabel) samen met een sleutelwoord om een bericht te coderen (encrypt) of te decoderen (decrypt). Bijvoorbeeld, stel we willen de volgende tekst coderen:
gebruik makend van het sleutelwoord BRUTUS, dan beginnen we met het sleutelwoord zo vaak als nodig boven de te coderen tekst te schrijven. Hierdoor krijgen we voor iedere letter uit de tekst, twee letters: een (cyclische) letter van het sleutelwoord en een letter uit de tekst. De letter van het sleutelwoord gebruiken we om de regel in de tabel te selekteren, de letter uit de tekst om de kolom te selekteren. In het gegeven voorbeeld geeft dit als resultaat:
sleutelwoord: BRUT USBR UTUS
Tekst: VENI VIDI VICI
Gecodeerde tekst: WVHB PAEZ PBWA
Merk hierbij op dat er een één op veel relatie is tussen de letters uit de gecodeerde tekst en de letters uit de oorspronkelijke tekst. Met andere woorden een letter uit de gecodeerde tekst kan corresponderen met een veelheid aan letters uit de ongecodeerde tekst. De corresponderende letter kan slechts gevonden worden met behulp van het sleutelwoord. Dit is een belangrijke eigenschap, want iedere taal heeft een bepaald frequentiepatroon waarin letters in woorden voorkomen. Met behulp van dit frequentiepatroon kunnen crypto-analisten een code breken door het frequentiepatroon van de gecodeerde tekst te onderzoeken en te vergelijken met het frequentiepatroon van de gebruikte taal (zo de taal bekend is). Het decoderen is hierna relatief eenvoudig. Het gebruik van de Vigenere cipher zorgt er echter voor dat het frequentiepatroon van de taal op zijn minst gedempt wordt, waarmee crypto-analyse bemoeilijkt wordt.
Het decoderen van de bovenstaande gecodeerde tekst is eenvoudig als het sleutelwoord bekend is. Gebruik de letter van het sleutelwoord om de regel te vinden en zoek in deze regel naar de letter uit de gecodeerde tekst. Het kolomhoofd van de kolom waarin de letter staat is de gedecodeerde letter.
Het gebruik van versleuteling neemt door de eeuwen heen steeds toe en wordt in het bijzonder gebruikt in diplomatieke kringen en - vanzelfsprekend - in militaire kringen.
Er zijn twee versleutelings grondvormen (zie [ 1 ,5 ]):
Bij substitutie versleuteling, worden de letters van een tekst vervangen door andere letters, door in een vaststaand alfabet een der letters een bepaald aantal posities te verschuiven.
De Caesar cipher is een voorbeeld van een substitutie versleuteling.
Bij transpositie versleuteling worden de letters van een tekst in een bepaalde volgorde herordend.
De scytale is een voorbeeld van een transpositie versleuteling.
Op beide grondvormen zijn verfijningen mogelijk. Ten eerste door de tekst niet eenmaal te versleutelen - hetgeen mono-alfabetische versleuteling wordt genoemd - maar door de tekst meerdere malen te versleutelen. Dit laatste wordt poly-alfabetische versleuteling genoemd. Het mag duidelijk zijn dat hiervoor verschillende alfabetten gebruikt moeten worden, anders voegt het gebruik ervan niets toe aan de complexiteit van de versleuteling.
Ten tweede is door het combineren van transpositie en substitutie versleuteling - al dan niet poly-alfabetisch - een complexere versleuteling te verkrijgen. In feite voegen we dan verschillende versleutelingsmethoden samen, met andere woorden: de totale versleuteling is het resultaat van het product van verschillende versleutelingen. Daarom wordt een dergelijke constellatie ook wel een product cipher genoemd. Een product cipher bestaat typisch uit een reeks aan elkaar geluste substitutie en transpositie combinaties (zie [ 1 ]). Een fractionation cipher is hiervan een voorbeeld. Een bijzondere klasse van product ciphers waren de zogenaamde fractionation ciphers waarbij de tekens uit de te coderen tekst eerst door middel van substitutie versleuteling door meerdere andere tekens vervangen werden, waarna deze `tussenresultaat-tekst` vervolgens door middel van een tranpositie versleuteling gecodeerd werd om de uiteindelijke versleutelde tekst te krijgen (zie [ 8 ] onder `cipher`).
Door deze verfijningen wordt een versleuteling dus complexer en is het dus minder eenvoudig de versleutelde tekst - zonder kennis van de gebruikte methode en de eventuele sleutel - te decoderen (kraken).
De Vigenère cipher is een voorbeeld van een poly-alfabetische substitutie versleuteling.
Het meest tot de verbeelding sprekende gebruik van geheimschrift is wel het gebruik van de enigma machine door de Duitsers in WO II. De enigma was een klasse van machines gebaseerd op een poly-alfabetische substitutie versleuteling. Het coderen gebeurde met behulp van een soort cipher disks. Deze disks werden rotors genoemd.
De enigma werd reeds in de vroege twintiger jaren van deze eeuw uitgevonden en op de markt gebracht. Omstreeks 1925 kocht de Duitse marine contracten van de enigma en rond 1928 werden de eerste gemodificeerde exemplaren aangeschaft. De enigma werd gebruikt om - ondermeer - met de U-boten te communiceren (zie [ 9 , 10 ]).

Een enigma machine
De enigma machine was gebaseerd op een systeem met drie rotors, die de tekstletters substitueerden tot gecodeerde letters. De rotoren hadden ieder 26 karakters (de letters van ons alfabet). De rotoren maakten gezamenlijk omwentelingen, in werking vergelijkbaar met de cijferbladen van een kilometerteller. Dus de tweede rotor draaide een stap als de eerste rotor een volledige omwenteling had gemaakt. De derde rotor draaide een stap als de tweede rotor een volledige omwenteling had gemaakt. Op deze wijze bood de enigma een op de caesar cipher gelijkende, variabele, versleuteling.
Wanneer een letter op het toetsenbord van de machine werd ingetikt, dan werd deze door de eerste rotor heen gezonden. De eerste rotor voerde een substitutie uit, welke afhankelijk was van de stand van de rotor. De nieuwe letter werd daarna door de tweede rotor gestuurd, alwaar wederom een substitutie werd uitgevoerd, afhankelijk van de stand van de tweede rotor. Het resultaat hiervan werd door de derde rotor gevoerd, waarin wederom een substitutie plaats vond. Daarna werd deze nieuwe letter door een reflector teruggestuurd door de drie rotors. Doordat de rotoren op de beschreven wijze verdraaiden na iedere toetsaanslag, werd effectief een poly-alfabetische versleuteling bereikt, waarbij na iedere toetsaanslag de versleutelings alfabetten verwisseld werden (zie [ 4 ]).
Om de versleutelde boodschap te kunnen ontsleutelen hoefde men `slechts' de initiele stand van de rotors (de sleutel) te kennen. Nadat deze op de juiste stand waren gezet kon de gecodeerde boodschap worden ingetikt. Doordat de machine - mede door gebruik van de reflector (zie [ 10 ]) - een symmetrisch karakter vertoonde, kon na intikken van iedere gecodeerde letter de ongecodeerde letter worden afgelezen. Met symmetrie wordt hier het volgende bedoeld:
X = decodeer(codeer(X))
De drie bewegende rotors kunnen 263 = 17576 mogelijk posities innemen. Dit samen met enkele andere aanpassingen die de Duitsers aan het oorspronkelijke apparaat aanbrachten, werd het aantal mogelijke versleutelingen met een factor van 2 tot 3 miljard verhoogd. Als een enigma te buit zou vallen en men zou 1000 mensen vier sleutels (rotor posities) per minuut laten testen gedurende 24 uur per dag, dan zou het hen 900 miljoen jaren kosten om alle mogelijke sleutels uit te proberen. Om deze reden waren de Duitsers ervan overtuigd dat hun codes onbreekbaar waren (zie [ 10 ]).
Waar de Duitsers echter niet op hadden gerekend, was dat de Polen hen al geruime tijd in de gaten hielden. Reeds in 1933 hadden de Polen een werkende replica van de enigma, dankzij het werk van Marian Rejewski, Jerzy Rózycki en Henryk Zygalski, welke op geniale wijze deze replica tot stand hadden gebracht. Gedurende de jaren wijzigden de Duitsers echter elementen van de enigma, waardoor de replica niet meer in staat was berichten te ontcijferen (decoderen). Het lukte de Polen tot twee maal aan toe om de wijzigingen te achterhalen en de enigma weer werkend te krijgen. De laatste maal lukte dit echter niet, mede door de Duitse inval in Polen. De drie vluchtten naar Frankrijk en namen hun replica en papieren mee (zie [ 10 , 11 ]).
Uiteindelijk belandde de informatie in Engeland bij het Ultra project (zie [ 8 , 9 ,10 , 11 ]). Daar werd door de brilliante geleerde Alan Turing, de enigma gekraakt.
Alhoewel Alan Turing de geschiedenis in gegaan is als de kraker van de enigma, hebben de Polen Marian Rejewski, Jerzy Rózycki en Henryk Zygalski eveneens een zeer belangrijke en substantiele bijdrage hieraan geleverd. Diverse bronnen gaan niet op de Poolse bijdrage in, of erger, vermelden blijkbaar onjuiste gegevens (zoals [ 8 ]). Voor een volledigere beschrijving van de geschiedenis en het kraken van de enigma verwijs ik naar [ 10 ] en de andere in dit hoofdstuk genoemde bronnen.
Op de ftp-site van mindlink zijn een groot aantal afbeeldingen van de enigma te verkrijgen.
Het is mogelijk om - indien uw browser applets kan verwerken - met een enigma simulatie te experimenteren. Kies hiertoe een van de twee navolgende verwijzingen.
Een van de - naar mijn mening - beste beschrijvingen is de beschrijving in [ 10 ].
Al het bovenstaande bronmateriaal en meer, behalve [ 8 ] (bedankt Math. Wielders), is gevonden door gebruik te maken van navolgende search-engines:
In alle gevallen is gezocht met behulp van de navolgende queries:
Daarnaast is in Altavista met de geavanceerde zoekopties door middel van booleaanse queries gezocht, bijvoorbeeld:
(cipher or crypto*) and (fractionation)
De queries op fractionation leverden alle geen relevante resultaten op. Nadat deze queries echter als volgt geformatteerd werden, werden er - merkwaardig genoeg - wel relevante verwijzingen gevonden.
"fractionation" +"cipher system"
Door de overweldigende hoeveelheid aan informatie op het World Wide Web is niet in nieuwsgroepen gezocht. Bovendien bevatte een groot aantal `query-resultaat-pagina's' doorverwijzingen naar andere relevante pagina's. Hierdoor is het in sommige gevallen onnodig verder te zoeken middels search-engines, omdat de auteurs van deze pagina's de moeite hebben genomen daadwerkelijk relevante links op te nemen.
Alle search engines zijn goed bruikbaar en geven goede resultaten.